At a depth approaching 200m radio-location is not easy. Brian Pease compares practical measurements using his beacon, to a theoretical model.
Introduction
This article
documents the difficulties involved in obtaining an accurate depth measurement
with a cave radio when the depth becomes large. The errors in estimating
depth build up roughly linearly with increasing frequency and increasing
conductivity of the earth but roughly as the square of increasing
depth. Multi-layered earth with jointed rocks of different conductivities
add to the fun! On a recent trip to West Virginia (USA) an attempt was
made to locate and measure the depth of a 3496Hz CW beacon located in a
cave passage about 670ft (207m) beneath a steep hillside. The purpose was
to double-check the cave survey which showed the end of the passage (Dream
Lake) to be at the same elevation as the known resurgence located several
km away. The rock at the surface was sandstone, followed by shale, and
finally limestone. The phase-locked "Double-Quadrature" receiver (Pease,
1996b) was used for this task due to its high sensitivity and ability to
give a digital read-out of the beacon’s magnetic field strength. Once ground-zero
was located – with some difficulty apparently due to anisotropic (directional)
conductivity effects – the depth was measured using three more or less
independent methods:
The Problem
The electrical
conductivity of the rock overlying a cave passage will cause errors in
any of the methods that might be used to find the depth of the passage
with a cave radio. Details of the three depth methods are given later.
A computer program (FATE-VMD) written by Steven Shope of Sandia Research
Associates, Inc in New Mexico, USA was used to compute the effect of conductivity
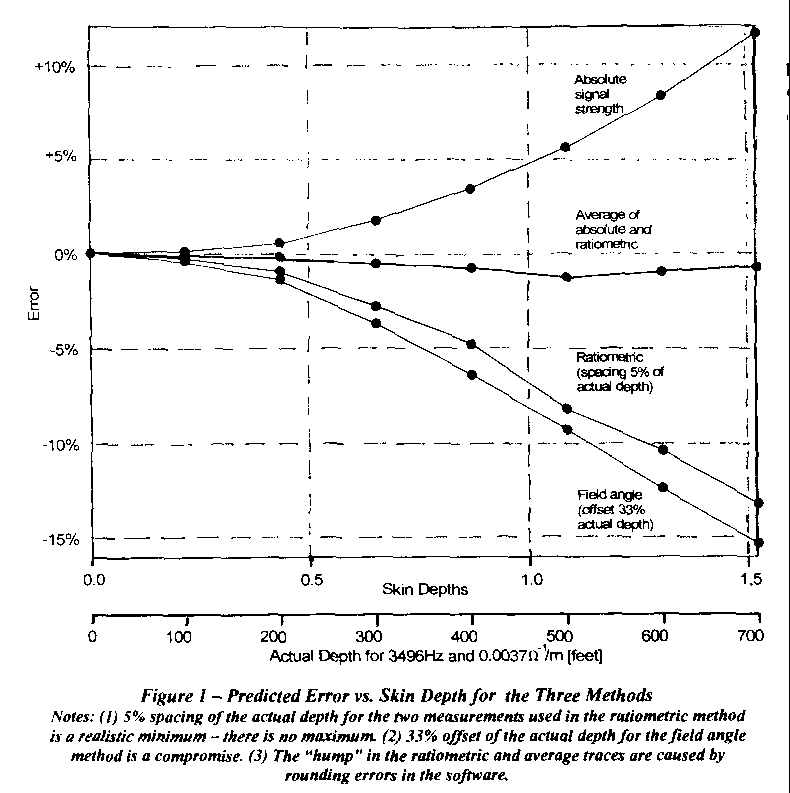
on the magnetic fields (Shope, 1991). Figure 1 gives the predicted depth
error v. skin depth for the three methods, assuming a homogeneous
(uniform) earth. A positive error means that the method in question will
over-estimate the depth. A second scale gives actual depths for a typical
conductivity of 0.0037W -1/m and a frequency
of 3496Hz. This scale shows the small errors (1% range) at a depth of 200ft
(60m) and the large errors (15% range) at the 670ft (207m) depth of Dream
Lake. For a given conductivity and frequency, the magnitude of the error
increases roughly as the depth squared. A fourth trace shows the much smaller
errors that result when the absolute and ratiometric methods are combined
by taking their average – again assuming homogeneous earth. I have no
mathematical basis for this averaging, I merely noticed that the two errors
always seemed to be approximately equal in amplitude and opposite in sign!
| 3496 Hz radio | 874 Hz Radio
(for comparison) |
|
| Magnetic Moment of Beacon | 44 Am2 | 20 Am2
(realistic guess) |
| Vertical field at ground-zero | 0.32 uA/m | 0.24 uA/m |
| Reading on DVM (1999 full scale) | 1101 | Unknown
(not built yet) |
| Signal at ground-zero compared to free space | -4.4 dB | -1.0 dB |
| Depth by Absolute signal strength
using free space equation |
888 ft (271m) | 781 ft (238m) |
| Ratio of signal at ground-zero to that
at 25 ft above ground zero |
1.1255 | 1.392 |
| Ratiometric depth using free space equation | 622 ft (190m) | 706 ft (215m) |
| Average of Absolute and Ratiometric
depth results |
755 ft (230m) | 743 ft (226m) |
| Vertical to horizontal field strength ratio on
surface at 300 ft offset from ground zero. |
1.155 | 1.392 |
| Vertical to horizontal phase difference | -19 degrees | -9.55 degrees |
| Approx. null depth at 300 ft offset | -15.5 dB | -21.6 dB |
| Null angle(from vertical) at 300 ft offset
calculated from vertical/horizontal ratio |
40.9 degrees | 35.7 degrees |
| Depth by Field Angle using free space equation | 594 ft (181m) | 693 ft (211m) |
Table 1 - Predicted Depth Results for 750 ft actual depth
and conductivity of
.005 S/m. Free space equations used
for the three depth methods.
To determine if my radio was up to the task I modelled the radio-location using Steven Shope’s program for a depth of 750ft (229m). I chose a conductivity of 0.005W -1/m after consulting local cavers to determine what rock types were present over the cave and searching the literature for typical conductivities, which were:
Sandstone 0.002W -1/m
Shale 0.008W -1/m
Limestone 0.0033W
-1/m
(most of the thickness)
Table 1 shows the depth predictions for each of the three methods I planned to use. As in Figure 1, Each depth "measurement" was done assuming "free space" conditions, ignoring conductivity, to see how large the errors would be for each method. The predictions for an 874Hz radio (not actually built yet) were done for comparison. I immediately concluded from this computer exercise that I really needed the lower frequency radio, but that I would try it anyway with my 3496Hz unit since the average of the absolute and ratiometric depth methods gave a reasonable result.
Receiver sensitivity was more than adequate. At a quiet location on a quiet day it would be limited only by the thermal noise of the loop which is equivalent to about 0.53nA/m in a 1Hz bandwidth.
A signal equal to this noise would produce a reading of "004" on the receiver’s DVM readout at the highest useable gain (1999 full-scale). Since the audio bandwidth is also 1Hz, this signal should be just audible at the noise level. The phase-locked loop would lock easily as its bandwidth is only 0.16Hz and the DVM readout would be reasonably steady since its bandwidth (in narrowest mode) is 0.04Hz. The expected beacon signal at ground-zero of 1101 on the DVM is 49dB above this minimum signal and 63dB above the noise in the readout’s 0.04Hz bandwidth. In the eastern USA power-line noise always seems to be the dominant noise source with atmospheric noise from thunderstorms sometimes a problem in afternoons and evenings.
The Cave
Culverson
Creek Cave, located in Greenbriar County, West Virginia, is a large cave,
currently being mapped and studied by the West Virginia Association for
Cave Studies (WVACS). When Phil Lucas of WVACS contacted me, I jumped at
the chance to try a really deep radio-location. The purpose of this radio-location
was to attempt to locate the point on the surface directly over Dream Lake
siphon, the lowest point in the Cave at nearly 700ft (213m) below the surface,
and to measure its depth so that its elevation could be determined. The
cave survey put Dream Lake at nearly the same elevation as the cave’s resurgence
at Spring Creek. Because Dream Lake is located 4km from the resurgence,
the hope was that the surveyed elevation was wrong and its elevation was
actually higher which would give some hope of air filled passage beyond.
We formed two
teams, with Phil and two others taking my 3496Hz beacon into the cave in
the morning for the three hour trip to Dream Lake while I and my friend
Peter Grant slept late and then drove close to the estimated location of
the ground-zero which was a mere 10 minute walk uphill. Cliff Lindsey from
WVACS showed up later. I was concerned about EMI from the power lines located
near the car and about atmospheric noise building up since it was almost
noon, but the digital field strength readout on my D-Q receiver indicated
only
2-3 (on a scale of 1999) at nearly full receiver gain
in its 1Hz mode.
I set the
receiver and its 460mm loop on the ground and we chatted until the alarm
sounded as it phase-locked to the continuous beacon signal about 20 minutes
later. The signal was very strong, nearly "1000" on the DVM, as predicted,
but then the fun began as I tried the usual technique for deep locations
of laying down two "lines of position" (LOPs). (Picture
and description). As I moved around, holding the loop vertical,
only one LOP gave a sharp and deep null with all other directions very
broad and shallow. The digital readout allowed me to locate the shallow
null directions, but all the ones I could try (given the steep hillside)
were nearly parallel and first led me uphill then back down again! Signal
strength readings were not much help either due to the steep hillside which
caused the cubic change with distance to swamp the smaller change as we
moved horizontally near ground-zero. Peter thought I was going crazy. I
finally gave up on the "two LOPs" method and relocated the LOP with the
sharpest null. I then reverted to the simple technique I use with shallow
caves which is to follow the LOP in one direction and occasionally stop
to turn the vertical loop perpendicular to the line of travel then null
the signal by tilting the loop towards or away from me to determine the
angle of the field lines as they leave the ground. This is the same method
used to determine depth by field angle. If you are headed towards ground-zero
the field will become more vertical at each stop with the signal strength
improving and nulls getting sharper. This technique got us to ground-zero
rapidly, where the field angle went exactly vertical, and was the only
way to tell that we had arrived because the vertical loop still gave a
strong null in the direction we had been travelling! This does not give
one a warm fuzzy feeling! More on this asymmetric effect later. We were
only about 150ft (46m) from where we had waited. I may do a study someday
on the use of briar patches to locate ground-zero quickly without bothering
with the cave radio!
Depth By Absolute
Field Strength
Once ground-zero
was located as closely as we could, the signal strength was measured by
simply placing the loop exactly horizontal on the ground and recording
the DVM reading and the receiver gain settings for later use in calculating
depth. Being precisely at ground-zero is not critical as the signal drops
off slowly as you move away from it. The D-Q Receiver has a precisely calibrated
gain control and is very linear and stable as nearly all of its gain occurs
in a.c.-coupled op-amps with strong feedback. It was calibrated prior to
the trip over low conductivity granite (0.0009W
-1/m) at 100ft (30m) spacing with both loops horizontal. The calibration
is essentially the same as "free space" at this short distance. The received
signal was multiplied by two to give a calibration suitable for use with
the coaxial loop arrangement used at the cave. Vertical coaxial loops on
the surface give a calibration even closer to free space, but I had no
way at the time to hold the 1.3m beacon loop circular while upright. This
is the easiest method to measure depth, as only one reading is needed,
but calibration is required before or after the trip and the beacon’s magnetic
moment and the receiver’s gain must not change during the trip.
Data
reduction consisted of calculating the (relative) receiver input voltages
for the 100ft calibration (Vcal) and the actual signal at ground-zero
(Vz). The depth, D, based on the free-space cubic fall-off
equation, ignoring the effect of conductivity, is simply:
where Dcal is the distance at which Vcal was measured (in this case 100ft).
The calculated
(relative) receiver input voltages were Vcal=860420 and Vz=1056
Using this "free space" equation gave a depth of 934ft (285m) which is
high, of course, due to the signal loss in the rock which makes the beacon
seem to be deeper than it really is.
Depth by Ratiometrics
This method
of depth measurement assumes that the signal in the air above ground-zero
exhibits the cubic fall-off of free space and again ignores any effects
of conductivity. This method, suggested to me by David Gibson, involves
measuring the signal strength at ground-zero and also at a known height
above it. As far as I know I am the first caver to use it in the field.
[Although
some UK commercial radio-location equip-ment uses this principle – DG].
The technique
involves recording the DVM reading of signal strength with the receive
loop horizontal on the surface (V1, the same reading used to calculate
depth by signal strength) and then raising the loop to a precise height
above the ground and recording the new reading (V2). Being precisely
at ground-zero is not critical for this measurement. No calibration of
the receiver is needed since the same gain setting can be used for both
readings and only the ratio of the two numbers is used to calculate
the depth. I feel that a height of 5% of the estimated depth is sufficient
with the resolution of my readout thus a 6ft low-stretch cord gives sufficient
height for depths to at least 120ft (36m) where the errors due to conductivity
are also minimal. I have made several of these shallow measurements and
feel it is the best and easiest technique to use. For this extreme depth
I was only able to raise the loop 25ft (8m)
using a 10 piece aluminium pole, which is about 3.5% of the estimated depth,
and we succeeded only because there was a handy tree at ground-zero to
steady it! A test was done before hand that showed that the metal pole
had no measurable effect on the receiver readings.
The calculation
is another variation of the cubic equation:
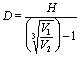
where H is the height between the two measurements (25ft in this case).
The raw numbers on the DVM were 1046 on ground-zero and 937 when raised 25ft, which gave a depth of 680ft (207m) ignoring the effects of conductivity. Computer experiments using Steven Shope’s program show that for a simple uniform conducting earth this method will make the beacon seem shallower than it really is.
Depth By Field Angle
This being the well-known traditional method I will not describe the technique. I only had time for a single measurement so there was no way to compensate for errors in the ground-zero location which is critical here. One also must survey from ground-zero to the measurement point. I simply walked away from ground-zero (in the only direction where I could stay roughly level with it) for about 250ft (76m) then measured the null angle (38.5degrees from vertical). The shallow null (16.7dB, about what I had predicted) was so broad that I had to use the DVM reading to find the centre. Because of this I also measured the relative horizontal (Vhor) and vertical field (Vver) strengths. I then marked the location with a stake. Later Peter and Cliff surveyed to this point from ground-zero and tied both to a known point on the topographical map. There are many possible sources of error in this technique.
Back at the nearby WVACS Fieldhouse, the survey data were reduced, which placed the field angle point 247ft horizontally and 16ft higher than ground-zero. This worked out to a beacon depth of 508ft (155m) using the free space equation. I was not happy with the broad null so I tried calculating the null angle from the ratio of the horizontal and vertical field strengths just as I did with the computer program. Using
where q is the field angle
from the vertical, gave me a figure of 31.1degrees in this case, which
corresponds to a depth of 647ft (197m) from ground-zero with the free space
equation. (The ratio is Vhoriz
/ Vvert if you can't read it). Strictly speaking,
a more complex equation taking the horizontal to vertical phase difference
into account should be used. This method is really useable only at shallow
depths where the sharp null can be used directly. At such depths all three
methods will give nearly identical results.
Conductivity
I measured the conductivity of the rocks near the surface at 66ft (20.2m spacing) using the D-Q Receiver and a spare beacon with a rigid loop (Pease, 1991; Drummond, 1989). This VMD (Vertical Magnetic Dipole) technique involves recording a reference level with both loops horizontal (Hz), then raising the receiver loop vertical with its axis aimed at the beacon, carefully finding the exact null, and recording the level (Hx). If the null depth is at least -24dB (16:1) then a simple formula:
yields conductivity directly. Here w is the angular frequency (= 2p f), m is the magnetic permeability of the rock (say equal to m 0, 4p x 10-7 H/m) and R is the distance between the transmitter and receiver. (The null depth decreases as the spacing increases.) The ratio is Hhoriz / Hvert if you can't read it.
In this case, we have f = 3496Hz, so the constant term is 145. The ratio Hx/Hz = 0.003634 (-49dB) so the conductivity is 0.0013W -1/m, which is reasonable for the sandstone cap-rock. I have found that conductivity tends to be lower on well-drained hillsides. The skin depth corresponding to this conductivity is 775ft (236m). More on conductivity later.
Postscript: At wider spacings ,
the simple equation presented here is not accurate. The plot given in Ian
Drummond's Article allows much wider spacings to measure conductivity at
greater depths. Under some conditions, the null will
occur with the loop not vertical (top tilted away from the Beacon). Just
ignore the tilt and use the null value as before.
| Measurements
over dream lake |
Calculations (based on
D=807ft, conductivity= 0.0037S/m, see text) |
|
| Depth by Absolute Signal strength | 934 ft(285m) | 934 ft (285m) |
| Ratio of signal at ground-zero to that at
25 ft above ground-zero |
1.1147 | 1.1142 |
| Ratiometric depth | 680 ft (207m) | 684 ft (208m) |
| Average of Absolute and Ratiometric depths | 807 ft (246m) | 809 ft (247m) |
| Vertical to horizontal field strength ratio at
247 ft offset from ground-zero and 16 feet above ground-zero |
1.655 | 1.685 |
| Null angle (from vertical) at 247 ft offset
calculated from vertical/horizontal ratio |
31.1 degrees | 30.7 degrees |
| Depth by Field Angle (from above data) | 647 ft (197m) | 659 ft (201m) |
| Null angle by direct measurement (for
reference, not used) |
38.5 degrees | |
| Null depth at 247 ft offset from ground zero
9for reference, not used) |
-16.7 dB | -17.8 dB |
Table 2 - Results of the Dream Lake 3496 Hz radio-location
compared to calculations
for homogeneous earth (free space calculations used in
each case). Actual depth
(based on survey): 670 ft (207 m) approximately.
Estimating Actual Depth From The Measurements
The extreme depth (around a skin depth for a 3496Hz radio) caused a large difference in the results of the three different depth methods. As mentioned earlier, this was predicted by the FATE-VMD computer program and shown in Table 1 for my pre-trip guesses of 750ft (229m) actual depth and overall conductivity of 0.005W -1/m. Note that the predicted average of the absolute and ratiometric methods for this homogeneous earth case is very close to the actual depth. There is no mathematical basis for this; it is merely an observation from experiments with the computer program!
Table 2 shows the results of the Dream Lake radio-location and compares them to the results of the FATE-VMD program for homogeneous earth. Based on the results in Figure 1, my best guess of the depth of the beacon was found by averaging the absolute and ratiometric results to get 807ft depth (246m) which unfortunately put Dream Lake 137ft (42m) below its resurgence if the surface survey is correct!
Ignoring this obvious error for the moment, the computer results are quite interesting. I assumed that 807ft was the actual depth to the beacon and worked "backwards" in the program to compute the average conductivity that gave the measured depth by absolute signal strength of 934ft, which was 0.0037W -1/m. I then used this conductivity and the 807ft to predict what depth I would obtain with the ratiometric method. This came out 684ft, almost exactly what was measured! As a final check, I computed the horizontal and vertical field strengths at 247ft horizontally from ground-zero (and 16ft above it) for 807ft depth and 0.0037W -1/m, then calculated the null angle as 30.7° from vertical which is almost dead on with the field measurement of 31° calculated from the two measured fields. That figure for conductivity implies a skin depth of 460ft (140m) which, of course, explains why the three methods give such different results, since there will be a significant far-field element to the fields.
Conclusions
By assuming that the real depth of the beacon is the average of the depths found by the absolute signal strength and the ratiometric methods (807ft), an "average" conductivity can be found, which seems to be a reasonable value. Using this depth and conductivity in Steven Shope’s Magnetic Field program causes the Dream Lake results to agree with the program very closely for all three depth measurement methods. The approximately 137ft (42m) overestimate of the depth of Dream Lake is most likely due to the multi-layered rock overlying the cave and also to the various layers beneath the beacon since the magnetic fields travel as far below the beacon as above it. Since Dream Lake is well over a skin depth below the surface, there are probably significant far-field components that are not taken into account in the FATE-VMD program. All three depth techniques will give erroneous results even in homogeneous earth unless the conductivity is known (or measured) and taken into account, although the errors are small for depths under 200ft (60m), where the depth is a small fraction of the skin depth. The technique of averaging the absolute and ratiometric depth numbers may give better results over uniform limestone than I obtained in the rugged terrain of the West Virginia mountains.
The best answer to improving accuracy at great depths is to use a lower frequency such as 874Hz (3496Hz divided by four) which should reduce depth errors by about a factor of 4 and make ground-zero location easier and more accurate by increasing null depths.
References
Drummond, Ian (1989) Ground Conductivity by Electromagnetic Methods, Speleonics 12, pp4-5, April 1989.
Gibson, David (1996) How Accurate is Radio-Location, Compass Points 10, pp5-9.
Pease, Brian (1991) Measuring Ground Conductivity with a Cave Radio, Speleonics 16, pp4-6, May 1991.
Pease, Brian (1996a) 3496Hz Beacon Transmitter & Loop, CREGJ 23, pp22-24.
Pease, Brian (1996b) The D-Q Beacon Receiver – Overview, CREGJ 24, pp4-6.
Shope, Steven M. (1991) A Theoretical Model of Radio-Location, The NSS Bulletin, Vol. 53, No. 2, p. 83-88, Dec. 1991.
Postscript: Report on Radio-location at Jewel Cave, South dakota, USA
From Cave Radio notebook, edited by David Gibson, in the BCRA CREG Journal 31, March 1998:
Brian Pease has done some more deep radio-location tests demonstrating his iterative technique, which is based on Steven Shope's simulation package (Shope 1991,)and my ratiometric equation (Gibson 1995). Brian's technique is potentially of great significance. I am intending to try to produce a theoretical justification for his results and an algorithm that 'bypasses' the need to do the iteration. Brian e-mailed me on 5th Jan.:
My refined estimate for the depth at the Jewel Cave radio-location station, near to survey point NY60, is 565'. As I recall, the estimate from the 'topo' was 550' for NY60 but the actual loop placement in the cave put us slightly uphill on the surface.
I began the iteration with 594', which
is the simple average of the depth by signal strength (762') and the 'ratiometric
depth' (426'). I used Steven Shope's program to calculate a rock conductivity
to fit the signal
strength data, making the assumption that 594' was the
real depth. I then calculated what the ratiometric depth would be, given
my measured data and this conductivity. Because the answer was not 594'
I tried a new depth (575') and kept iterating until both depth methods
gave the same depth result. This occurred at 565+/-5' with a conductivity
of 16.5mS/m. This conductivity can be thought of as a sort of average value
for a sphere with a radius of 565' centred on the underground beacon. It
is not as accurate as the number of digits suggests.
Since I had measured the vertical and
horizontal fields 200' from ground-zero (in two opposite directions on
the surface), I used the computer program to calculate the conductivity
needed to give the average
vertical/horizontal field ratio that I had measured.
I got a conductivity of 9.2mS/m. This result might have been different
if I had gone in different directions, as the rock was definitely anisotropic.
I noticed differences in the null depth as ground-zero was approached from
different directions, but couldn't measure the difference due to atmospheric
noise with the receiver loop vertical. At another location in Jewel (Spooky
Hollow, around 325ft deep), I got 6-10dB differences in null depths.
Direct conductivity measurements made
on the surface over the cave at spacings of less than 500' gave values
of around 5mS/m.
I guess it is reasonable to assume that the conductivity
of the limestone below the cave is higher than the limestone above it since
it should contain more water.
It is an interesting way to estimate
conductivity. The Conditions at Jewel Cave are somewhat favourable with
a lot of limestone both below and above the beacon, and terrain that is
gently rolling. There are other rocks(sandstone) near the surface and well
below the cave. The conditions at Culverson Creek Cave (Pease 1997) were
unfavourable enough that both depth measurements were deeper than the actual
depth could be, so the
method doesn't always work.
Brian Pease